UNITY (programming language)
UNITY is a programming language that was constructed by K. Mani Chandy and Jayadev Misra for their book Parallel Program Design: A Foundation. It is a rather theoretical language, which tries to focus on what, instead of where, when or how. The peculiar thing about the language is that it has no flow control. The statements in the program run in a random order, until none of the statements causes change if run. This allows for programs that run indefinitely (auto-pilot or power plant safety system) as well as programs that would normally terminate (which here converge to a fixed point).
Contents |
Description
All statements are assignments, and are separated by #. A statement can consist of multiple assignments, of the form a,b,c := x,y,z, or a := x || b := y || c := z. You can also have a quantified statement list, <# x,y : expression :: statement>, where x and y are chosen randomly among the values that satisfy expression. A quantified assignment is similar. In <|| x,y : expression :: statement >, statement is executed simultaneously for all pairs of x and y that satisfy expression.
Examples
Bubble sort
Bubble sort the array by comparing adjacent numbers, and swapping them if they are in the wrong order. Using 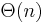 expected time,
expected time, 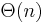 processors and
processors and 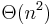 expected work. The reason you only have
expected work. The reason you only have 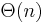 expected time, is that
expected time, is that k is always chosen randomly from 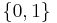 . This can be fixed by flipping
. This can be fixed by flipping k manually.
Program bubblesort
declare
n: integer,
A: array [0..n-1] of integer
initially
n = 20 #
<|| i : 0 <= i and i < n :: A[i] = rand() % 100 >
assign
<# k : 0 <= k < 2 ::
<|| i : i % 2 = k and 0 <= i < n - 1 ::
A[i], A[i+1] := A[i+1], A[i]
if A[i] > A[i+1] > >
end
Rank-sort
You can sort in 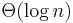 time with rank-sort. You need
time with rank-sort. You need 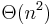 processors, and do
processors, and do 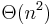 work.
work.
Program ranksort
declare
n: integer,
A,R: array [0..n-1] of integer
initially
n = 15 #
<|| i : 0 <= i < n ::
A[i], R[i] = rand() % 100, i >
assign
<|| i : 0 <= i < n ::
R[i] := <+ j : 0 <= j < n and (A[j] < A[i] or (A[j] = A[i] and j < i)) :: 1 > >
#
<|| i : 0 <= i < n ::
A[R[i]] := A[i] >
end
Floyd–Warshall algorithm
Using the Floyd–Warshall algorithm all pairs shortest path algorithm, we include intermediate nodes iteratively, and get 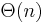 time, using
time, using 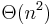 processors and
processors and 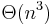 work.
work.
Program shortestpath
declare
n,k: integer,
D: array [0..n-1, 0..n-1] of integer
initially
n = 10 #
k = 0 #
<|| i,j : 0 <= i < n and 0 <= j < n ::
D[i,j] = rand() % 100 >
assign
<|| i,j : 0 <= i < n and 0 <= j < n ::
D[i,j] := min(D[i,j], D[i,k] + D[k,j]) > ||
k := k + 1 if k < n - 1
end
We can do this even faster. The following programs computes all pairs shortest path in 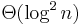 time, using
time, using 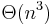 processors and
processors and 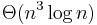 work.
work.
Program shortestpath2
declare
n: integer,
D: array [0..n-1, 0..n-1] of integer
initially
n = 10 #
<|| i,j : 0 <= i < n and 0 <= j < n ::
D[i,j] = rand() % 10 >
assign
<|| i,j : 0 <= i < n and 0 <= j < n ::
D[i,j] := min(D[i,j], <min k : 0 <= k < n :: D[i,k] + D[k,j] >) >
end
After round  ,
, D[i,j] contains the length of the shortest path from  to
to  of length
of length  . In the next round, of length
. In the next round, of length  , and so on.
, and so on.
References
- K. Mani Chandy and Jayadev Misra (1988) Parallel Program Design: A Foundation.